Fisica e matematica: l'irragionevole efficacia dell'ottimismo
Il 5 ottobre scorso il nostro Paese si è distinto per l’ennesima soddisfazione grazie alla conquista del Nobel per la fisica di Giorgio Parisi.
Le sue scoperte sono tra i contributi più importanti alla teoria dei sistemi complessi e consentono di comprendere e descrivere molti materiali e fenomeni diversi e apparentemente del tutto casuali. Tali sistemi sono stati oggetto di studio da almeno due secoli, scontrandosi contro la loro complessità matematica dovuta al fatto che possono avere un numero enorme di componenti e che il loro comportamento è spesso legato alle piccole variazioni nelle loro condizioni iniziali che si evolvono in grandi differenze imprevedibili in stadi successivi. Ne è un esempio perfetto il clima: “Può il batter d’ali di una farfalla in Brasile provocare un tornado in Texas?”, chiedeva provocatoriamente in proposito il matematico statunitense Edward Lorenz nel 1972. I “compagni” di Nobel di Parisi, il giapponese Syukuro Manabe e il tedesco Klaus Hasselmann, hanno sviluppato modelli fisici e matematici che consentono di prevedere con affidabilità le evoluzioni del clima terrestre, dandoci la certezza che il cambiamento climatico è purtroppo attribuibile alla nostra avventatezza. Giorgio Parisi si è invece concentrato sui cosiddetti vetri di spin, sistemi complessi e disordinati, la cui comprensione trova applicazione anche in fenomeni e campi apparentemente lontani, tra cui la biologia, le neuroscienze e il machine learning.

I vincitori del premio Nobel per la fisica 2021
Un suo predecessore, l’ungherese Eugene Wigner, premio Nobel per la fisica (1963) per i suoi contributi alla teoria dei nuclei atomici e delle particelle elementari, nel suo libro “L’irragionevole efficacia della matematica nelle scienze naturali”, sottolinea l’importanza del Numero nella descrizione della realtà.
La matematica, a suo dire, è fondamentale per la conoscenza della natura e svolge un ruolo “irragionevolmente importante in fisica”.
Gli attori sono tuttavia differenti: il matematico sfiora l’inammissibilità mentre il fisico è interessato a scoprire le leggi della natura inanimata che riguardano la regolarità degli eventi (proprietà dell’invarianza). La matematica viene utilizzata in fisica per valutare le conseguenze delle leggi di natura, ma la prima è fondamentale per la fisica in quanto “le leggi di natura, per poter essere usate, devono essere formulate in linguaggio matematico”.

Credits: Pexels.com
Un esempio lampante è stato l’utilizzo della legge della caduta dei gravi di Galileo: collegata da Newton al moto lunare, permise a quest’ultimo di osservare che il percorso(parabola) di un sasso lanciato sulla terra e quello della Luna nel cielo “sono casi particolari dello stesso oggetto matematico”. Dunque secondo Wigner “il miracolo dell’appropriatezza del linguaggio della matematica nella formulazione delle leggi della fisica, è un dono meraviglioso che non comprendiamo né meritiamo”. Per non cedere alla tentazione di cadere dalla torre di Pisa come oggetti di esperimenti galileiani, dovremmo considerare che la matematica può rappresentare spesso una via d’uscita ricordando il matematico francese D’Alembert che nel 1700 ideò un sistema progressivo utilizzato nelle scommesse diretto ad evitare perdite economiche rovinose! Le sue parole: “Calcola, la fede ti verrà!” sono state rielaborate alcuni secoli dopo nel meglio noto monito per gli studenti di meccanica quantistica “Zitto e calcola!”. Eppure anche Wigner, interessatosi come Parisi ai sistemi complessi, considerava la descrizione del loro comportamento molto più farraginosa di quella della loro struttura, manifestando un forte pessimismo in merito alla possibilità di giungere, dalle numerose teorie fisiche, ad una teoria ultima onnicomprensiva. Felici che l’ottimismo sia stato il sale della vita di un italiano.
Credits Copertina: Saad Ahmad su Unsplash
Leggi anche
"Chiamiamo licei gli istituti industriali". Leonardo Durante racconta i suoi progetti e i suoi robot
Il professore insegna Sistemi automatici e controlli all'Istituto tecnico industriale statale Enrico Fermi di Roma.
FL dà voce ai ragazzi sulla riforma scolastica e le materie STEM
A scuola di scienza: gli studenti del Liceo Kennedy di Roma coinvolti nel progetto di FL ed Edulia
Aerospazio, Difesa e Sicurezza. Orgoglio italiano
Alla fine del II millennio a. C., in Egitto, il tessitore Hapù pubblica in un papiro un annuncio di ricerca di uno schiavo fuggito offrendo una taglia.
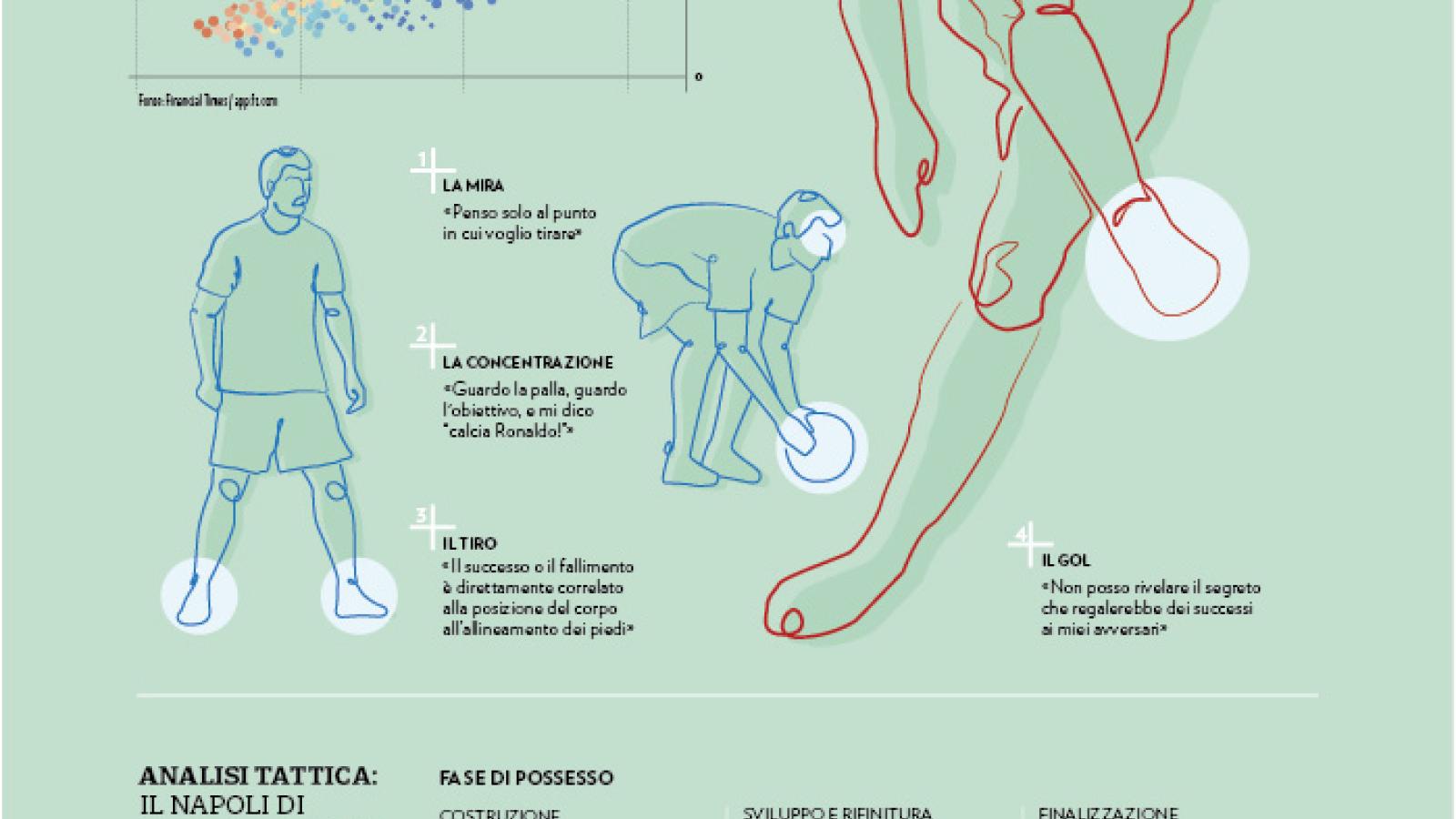
Algoritmi per fare gol. Intervista al leader calmo
Carlo Ancelotti da Reggiolo. È uno dei simboli del made in Italy.