La Successione di Fibonacci: simbolo razionale dell’energia materica nell’irrazionale eleganza dei processi organici

Una mania tutta americana quella di celebrare matematici vintage, traendo dall’ordine della datazione giornaliera anglosassone costanti matematiche e successioni numeriche.
Su modello del Pi greco day, che ricorre il 14 marzo (3.14), oggi onoriamo Fibonacci. I due numeri indicanti il mese di novembre prima (11) e il giorno (23) poi, posizionati uno dopo l’altro (1, 1, 2, 3, …) rappresenterebbero ̶ infatti ̶ le prime cifre di quella serie numerica nota come “successione Fibonacci”. Ma i conigli che c’entrano?
Figlio di Bonacci (da cui l’etimologia latina del nome), Leonardo Pisano fu un personaggio cruciale nella cultura matematica d’epoca medievale. «La sua maggiore intuizione», sottolinea la fisica Anna Parisi, «è stata introdurre in Europa le cifre allora chiamate “arabe” e quindi la notazione posizionale per la scrittura dei numeri. Il padre, infatti, era mercante e trafficava con gli arabi; il giovane Leonardo, che viaggiava con lui, si rese immediatamente conto che gli Arabi impiegavano pochissimo tempo a fare somme e sottrazioni proprio perché facevano le operazioni in colonna, cosa che non era possibile coi numeri romani ancora usati in Europa.»
«Quando mio padre, scrivano pubblico presso la dogana di Bugia per conto dei mercanti pisani», scrisse lo stesso Fibonacci nel Liber abbaci, «fu incaricato di dirigerla, essendo io ancora fanciullo mi fece andare presso di lui. Essendosi reso conto dell’utilità e dei vantaggi che me ne sarebbero venuti in seguito, volle che là per un certo tempo stessi a studiare l’abbaco e su esso venissi istruito.»
E fu proprio per tramite di questo libro, da lui scritto nel 1202, che i principi della matematica indo-araba (le cifre arabe, come si scoprì più tardi, erano di fatto cifre che gli arabi avevano imparato dagli indiani) confluirono nella nostra cultura e resero il testo un vero manuale di ragionamenti commerciali che ne decretarono il successo presso un pubblico molto più ampio dei testi matematici che lo avevano preceduto.

Una pagina del Liber Abaci di Fibonacci dalla Biblioteca Nazionale di Firenze
Compenetrato nelle disquisizioni matematiche e convintamente proteso al cambiamento, Fibonacci introdusse la numerazione araba nelle attività quotidiane dei mercanti, diffondendone l’utilizzo anche nell’uso manuale del far di conto. Fu così che Federico II, Imperatore del Sacro Romano Impero e Re di Sicilia, uomo colto, coltissimo, assolutamente devoto al confronto, rapito dai numeri tanto quanto dalle donne (dicunt) lo addentrò in un acceso dibattito matematico con gli studiosi della sua corte fino a quando ̶ ed eccoci ai conigli ̶ nella risoluzione di uno dei quesiti posti nel capitolo XXII del Liber Abbaci ̶ come evidenziato da Raffaella Franci nel Bollettino dell’Unione Matematica Italiana (Serie 8, Vol. 5-A—La Matematica nella Società e nella Cultura (2002), n.2, p. 293–328) ̶ non ebbe a calcolare «Quot paria coniculorum in uno anno ex uno pario germinantur» (quante coppie di conigli sono generati in un anno a partire da una coppia data) e fu durante la risoluzione di questo problema che vennero fuori i primi 12 numeri di quella che per primo Eduard Lucas, nel 1877, sembra aver nominato “successione Fibonacci”. Questa, spiega ancora la Parisi, «è una serie composta da numeri interi il cui nuovo termine viene calcolato dalla somma dei due termini precedenti a partire dai primi due che sono 0 e 1.
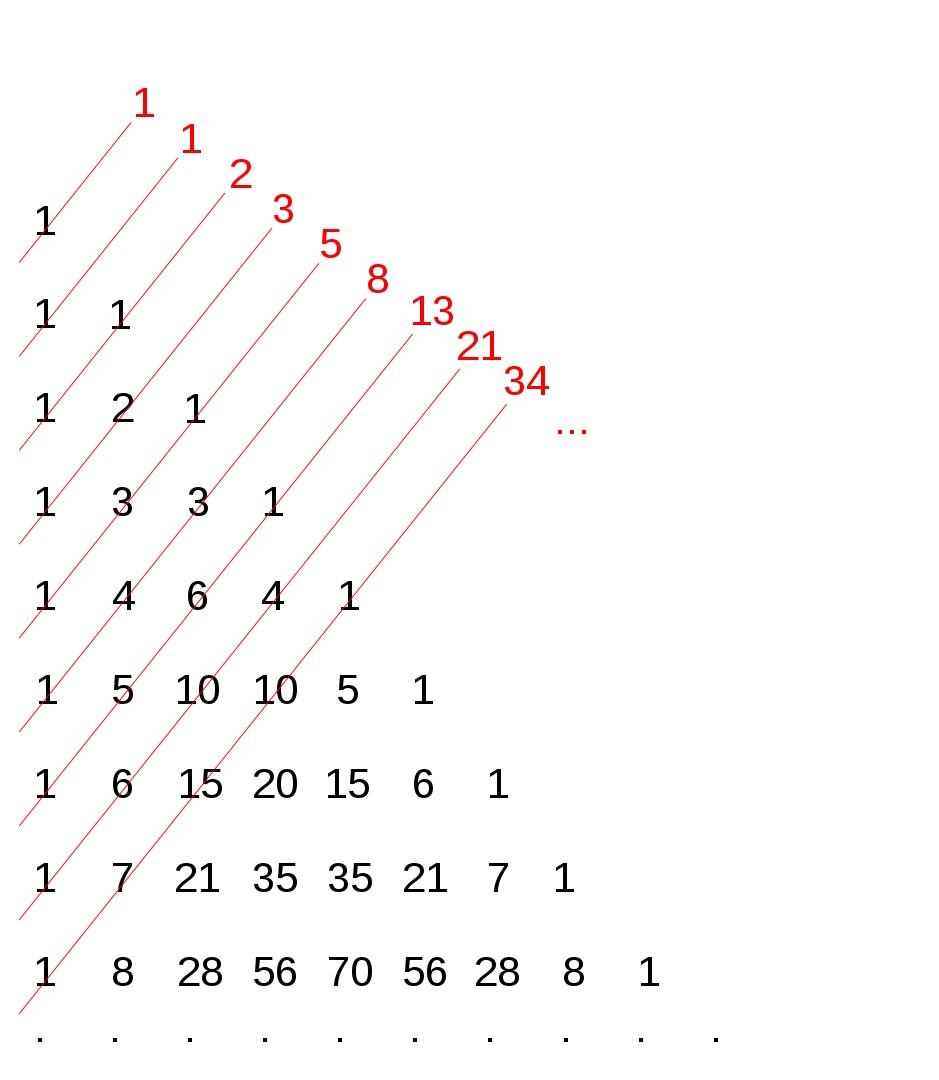
Serie di Fibonacci ricavata dal triangolo di Tartaglia. Crediti: Theon
Leonardo la scoprì analizzando la riproduzione dei conigli, supponendo che questi non abbiano figli il loro primo mese di vita e che poi facciano una coppia di figli ogni mese successivo. Ovviamente il calcolo è ideale in quanto ogni coppia di conigli che nasce deve essere costituita da un maschio e una femmina e nessun coniglio deve essere sterile né morire. Così facendo il primo mese abbiamo zero conigli (0) e il secondo abbiamo una coppia (1) che non ha figli e quindi il terzo mese abbiamo sempre una coppia (1). Il quarto mese abbiamo la coppia di genitori e la prima coppia di figli (1+1=2). Il quinto mese abbiamo la coppia dei genitori, la seconda coppia di figli dei genitori, la coppia dei primi figli che non hanno ancora figli (1+1+1=3), fino a raggiungere una serie infinita di numeri 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 …»
Tale serie, dimenticata nel tempo, sarebbe stata connessa alcuni secoli dopo, da Albert Girard, al numero aureo, un numero irrazionale dal valore 1,6180339887 che risulta approssimato al meglio proprio dal rapporto di due termini consecutivi della serie numerica di Fibonacci.
Uno sposalizio assolutamente riuscito, un amorevole connubio in cui l’irrazionale tende a migliorarsi fino a raggiungere la sua perfezione in natura nella circolarità di forme e movimenti, secondo una spirale logaritmica costruita su rettangoli. Un concetto tanto semanticamente complesso quanto semplicemente percepibile nella conchiglia del Nautilus, nelle corolle dei fiori, nella perfezione divina dei corpi fidiaci o dell’uomo vitruviano di Leonardo da Vinci. Un sillogismo aristotelico che definisce i labili confini fra filosofia e matematica, tra arte e scienza, che accorcia le distanze fra numeri e materia, in una visione quasi onirica, monumentalmente espressa nel “Volo dei numeri” di Mario Merz sulla Mole Antonelliana.
Una trasposizione logico-matematica, la serie Fibonacci, che nell’irrazionale eleganza dei processi organici diviene simbolo razionale dell’energia materica, nei processi di quell’infinita trasformazione naturale che è l’inspiegabile magia della vita.
Leggi anche
"La valle oscura": vivere e morire nella Silicon Valley
Da tempo ormai la Silicon Valley è al centro delle attenzioni, spesso ossessive, di opinione pubblica, intellettuali, politici e semplici curiosi.
5G, la tecnologia plasma il futuro: l'umanità è un'appendice superflua
Gli spot sulla nuova rete internet sono il manifesto dell'ideologia tecnocratica: la fantascienza è già scienza.
Ambivalenza o equivalenza
Se in una chat attribuite umanità al vostro interlocutore, e questi si rivela una macchina, allora si tratta di una macchina intelligente. Un’intelligenza artificiale.
Astronavi sulle spighe
Peppino Caldarola – già redattore presso il catalogo Laterza, due volte a capo de “l’Unità”, direttore di “Civiltà delle Macchine” – è stato un comunista.



